| By Lawrence Martin, M.D., FACP, FCCP Associate Professor of Medicine Case Western Reserve University School of Medicine Cleveland, Ohio Disclaimer |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
Abbreviations used:
|
|||||||||||||||||||||||||||||||||
S U M M A R Y TopFour equations are taught briefly in medical school but are grossly under-emphasized in importance and are therefore invariably forgotten in later years, when they are most needed. The reasons why these highly important equations are ‘under taught’ in medical school are several:
These four equations express relationships that are extremely important in clinical practice. They are the:
Emphasis should be placed on understanding the simple qualitative relationships expressed by these equations. Each equation can be clinically applied in the assessment of abnormal oxygenation, ventilation, or acid-base balance. For example, variables in the PCO2 equation, and not any bedside observations, define the common terms hyperventilation and hypoventilation and explain why a dyspneic, tachypneic patient may be retaining CO2. Ignorance of this and other relationships expressed in the four equations is reflected in some common diagnostic and therapeutic mistakes. INTRODUCTION There is disparity between the physiology we teach and expect medical students to learn and the physiology that medical residents and practicing physicians seem to know and understand. This disparity is perhaps best exemplified by four simple equations important in understanding cardiopulmonary and renal disorders (Table I). These equations are seldom emphasized beyond medical school, yet not appreciating the physiology behind them can (and often does) lead to clinical errors. Intensive care units have contributed to the weakening knowledge of physiology among primary care physicians. Today, the more profound physiologic derangements are usually managed in ICUs by organ-specific specialists; these derangements (e.g., shock, pulmonary edema, acute ventilatory failure, acute renal failure) are literally outside the care of most physicians and surgeons. Not all serious physiologic problems are handled in ICUs however, and the need for understanding basic physiology – in the office, on the general medical wards – remains paramount. The four equations in this paper (Table I, below) are important clinically not so much for the numbers they generate as for their qualitative relationships. All four equations can be abbreviated to simpler terms that are adequate for most clinical purposes.
|
|||||||||||||||||||||||||||||||||
| 1. The PCO2 Equation TopThe PCO2 equation puts into physiologic perspective one of the most common of all clinical observations: a patient’s respiratory rate and breathing effort. The equation states that alveolar PCO2 (PACO2) is directly proportional to the amount of CO2 produced by metabolism and delivered to the lungs (VCO2) and inversely proportional to the alveolar ventilation (VA). While the derivation of the equation is for alveolar PCO2, its great clinical utility stems from the fact that alveolar and arterial PCO2 can be assumed to be equal. Thus: | |||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| The constant 0.863 is necessary to equate dissimilar units for VCO2 (ml/min) and VA (L/min) to PACO2 pressure units (mm Hg). Alveolar ventilation is the total amount of air breathed per minute (VE; minute ventilation) minus that air which goes to dead space per minute (VD). Dead space includes all airways larger than alveoli plus air entering alveoli in excess of that which can take part in gas exchange. Even when alveolar and arterial PCO2 are not equal (as in states of severe ventilation-perfusion imbalance), the relationship expressed by the equation remains valid: | |||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
In the clinical setting we don’t need to know the actual amount of CO2 production or alveolar ventilation. We just need to know if VA is adequate for VCO2; if it is, then PaCO2 will be in the normal range (35-45 mm Hg). Conversely, a normal PaCO2 means only that alveolar ventilation is adequate for the patient’s level of CO2 production at the moment PaCO2 was measured. From the PCO2 equation it is evident that a level of alveolar ventilation inadequate for CO2 production will result in an elevated PaCO2 (> 45 mm Hg; hypercapnia). Thus patients with hypercapnia are hypoventilating (the term hypoalveolarventilating would be more appropriate but hypoventilating is the conventional term). Conversely, alveolar ventilation in excess of that needed for CO2 production will result in a low PaCO2 (< 35 mm Hg; hypocapnia) and the patient will be hyperventilating. (Confusion sometimes arises because the prefix (hyper-, hypo-) differs for the same condition depending on whether one is describing a blood value or the state of alveolar ventilation.) For reasons that will be discussed below, the terms hypo- and hyper- ventilation refer only to high or low PaCO2, respectively, and should not be used to characterize any patient’s respiratory rate, depth, or breathing effort.From the PCO2 equation it follows that the only physiologic reason for elevated PaCO2 is a level of alveolar ventilation inadequate for the amount of CO2 produced and delivered to the lungs. 1 Thus arterial hypercapnia can always be explained by:
Excess CO2 production is omitted as a specific cause of hypercapnia because it is never a problem for the normal respiratory system unimpeded by a resistive load. During submaximal exercise, for example, where CO2 production is increased, PaCO2 stays in the normal range because VA rises proportional to the rise in VCO2. With extremes of exercise (beyond anaerobic threshold) PaCO2 falls as compensation for the developing lactic acidosis.2 In health PaCO2 may be reduced but is never elevated. An important clinical corollary of the PaCO2 equation is that we cannot reliably assess the adequacy of alveolar ventilation – and hence PaCO2 – at the bedside. Although VE can be easily measured with a handheld spirometer (as tidal volume times respiratory rate), there is no way to know the amount of VE going to dead space or the patient’s rate of CO2 production. A common mistake is to assume that because a patient is breathing fast, hard and/or deep he or she must be “hyperventilating.” Not so, of course.
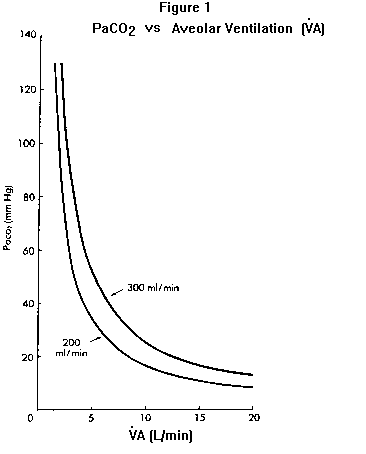
Although nothing in the PCO2 equation directly relates respiratory rate or depth of breathing to PaCO2, physicians commonly (and mistakenly) use these observations to assess a patient’s PaCO2. The error in this case was to assume the patient was hyperventilating (because she was breathing fast) and could tolerate the sedative; in fact she was hypoventilating – her PaCO2 was elevated (as will be explained further under Equation 2). Hypercapnia represents a failure of the respiratory system in some aspect and therefore a state of severe organ system impairment. In addition to this clinical fact there are three physiologic reasons why elevated PaCO2 is potentially dangerous. First, as PaCO2 increases, unless HCO3– also increases by the same degree pH will fall (see Equation 2). Second, as PaCO2 increases PAO2 (and hence PaO2) will fall unless inspired oxygen is supplemented (see Equation 3). Third, the higher the PaCO2, the less defended is the patient against any further decline in alveolar ventilation. This last point is graphically illustrated by plotting PaCO2 against alveolar ventilation Figure 1. The higher the PaCO2 is to begin with, the more it will rise for any given decrement in alveolar ventilation. For example a decrease in alveolar ventilation of one L/minute (as may occur from anesthesia, sedation, congestive heart failure, etc.) will increase a baseline PaCO2 of 30 mm Hg to 36.3 mm Hg when VCO2 is 200 ml/min; the same one L/min decline in VA will raise a baseline PCO2 of 60 mm Hg to 92 mm Hg Figure 1). Whereas the hyperventilating or normally- ventilating patient can almost always tolerate sedating drugs (without clinically important hypoventilation), even a small amount of sedative may be dangerous in the hypercapnic patient. Note also from Figure 1 that an increase in CO2 production (e.g., from 200 to 300 ml/min) without concomitant increase in VA (as should occur normally) will cause PaCO2 to increase. This situation is sometimes seen in patients with severe chronic obstructive lung disease when they exercise, and in artificially-ventilated patients who are carbohydrate loaded (which increases CO2 production). The basic mechanism for hypercapnia in these and all other cases, however, is inadequate VA for the amount of CO2 delivered to the lungs. |
|||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||
| 2. The Henderson-Hasselbalch Equation TopOf the four equations in this paper, the Henderson-Hasselbalch is the one with which physicians are most familiar. The H-H equation is repeatedly emphasized in basic science courses and in renal and pulmonary pathophysiology lectures; students hear about it on many occasions. The bicarbonate buffer system, quantitatively the largest in the extracellular fluid, instantaneously reflects any blood acid-base disturbance in one or both of its buffer components (HCO3– and PACO2). The ratio of HCO3– to PACO2 determines pH and therefore the acidity of the blood: |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
pH is the negative logarithm of the hydrogen ion concentration, [H+], in nM/L (nM = nanomole = 1 x 10-9 moles; pH 7.40 = 40 nM/L [H+]). Because of the negative logarithm, small numerical changes of pH in one direction represent large changes of [H+] in the other direction (Table II). An 0.1 unit fall in pH from 7.4 to 7.3 represents a 25% increase in [H+]; a similar percentage change in serum sodium would increase its value from a normal 140 mEq/L to 175 mEq/L!
Unfortunately, the logarithmic nature of pH and the fact that acid-base disorders involve simultaneous changes in three biochemical variables and in the function of two organ systems (renal and respiratory), have all combined to made acid-base a difficult subject for many clinicians. In the 1970s nomograms incorporating the H-H variables and compensation bands for the four primary acid-base disorders were introduced as aids to determining a patient’s acid-base status.3-8 While nomograms can be helpful if readily available and properly used, there is much to be gained by simply knowing the relationship among the three H-H variables and the type of changes expected with each disorder. In this regard the following items of clinical importance bear emphasis. a) If any of the three H-H variables is truly abnormal the patient has an acid-base disturbance without exception. Thus any patient with an abnormal HCO3– or PaCO2, not just abnormal pH, has an acid-base disorder. Most hospitalized patients have at least one bicarbonate measurement as part of routine serum electrolytes; this is usually called the ‘CO2‘ or ‘total CO2‘ when measured in venous blood. (Total CO2 includes bicarbonate and the CO2 contributed by dissolved carbon dioxide, the latter 1.2 mEq/L when PaCO2 is 40 mm Hg. For this reason, and because bicarbonate concentration is slightly higher in venous than in arterial blood, total CO2 runs a few mEq/L higher than the bicarbonate value calculated using the H-H equation.) If total CO2 is truly abnormal the patient has an acid-base disorder. In Case 1 there were two sets of electrolyte measurements on the patient’s chart when the sedative was ordered; both showed total CO2 elevated at 34 mEq/L. The patient had been taking a diuretic so it was probably assumed that her elevated total CO2 reflected a mild metabolic alkalosis. More likely, however, it represented chronic respiratory acidosis with renal compensation. When she arrived to the ICU her arterial blood gas showed pH 7.07, PaCO2 83 mm Hg, PaO2 55 mm Hg (breathing supplemental oxygen), HCO3– 23 mEq/L, values that reflected a worsening of previously- unrecognized respiratory acidosis plus a new metabolic acidosis (lactic acidosis from decreased organ perfusion). The patient’s long smoking history and the physical findings suggested chronic obstructive lung disease (later confirmed by pulmonary function tests). Her anxiety prior to MICU transfer was related to worsening acidosis and dyspnea. b) The simplified version of the H-H equation eliminates the log and the pK, and expresses the relationships among the three key values. |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| This version is sufficient for describing the four primary acid-base disturbances and their compensatory changes listed in Table III (below). If the numerator is first to change the problem is either metabolic acidosis (reduced HCO3–) or metabolic alkalosis (elevated HCO3–); if the denominator is first to change the problem is either respiratory alkalosis (reduced PaCO2) or respiratory acidosis (elevated PaCO2). TABLE III. The four primary acid-base disorders and their compensatory changes. The primary event leads to a large change in pH (larger arrows). Compensation (changes in HCO3– and PaCO2 represented by smaller arrows) attempts to normalize the ratio of HCO3–/PaCO2 and bring the pH back toward normal (smaller arrows next to pH). Each primary disorder may be caused by a variety of specific clinical conditions (see text). |
|||||||||||||||||||||||||||||||||
Top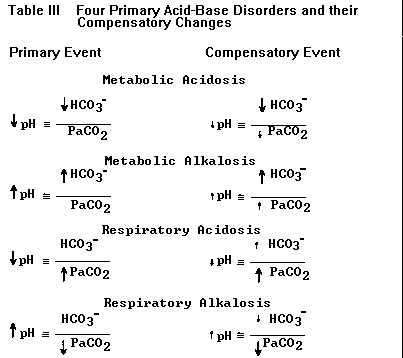 |
|||||||||||||||||||||||||||||||||
| c) By convention ‘acidosis’ and ‘alkalosis’ refer to in-vivo physiologic derangements and not to any change in pH. Each primary acid-base disorder arises from one or more specific clinical conditions, e.g., metabolic acidosis from diabetic ketoacidosis or hypoperfusion lactic acidosis; metabolic alkalosis from diuretics or nasogastric suctioning; etc. Thus the diagnosis of any primary acid-base disorder is analogous to diagnoses like “anemia” or “fever”; a specific cause must be sought in order to provide proper treatment. Because of the presence of more than one acid-base disorder (‘mixed disorders’) a patient with any acidosis or alkalosis may end up with a high, low or normal pH. For example, a patient with obvious metabolic acidosis from uremia could present with a high pH due to a concomitant metabolic alkalosis (which may not be as clinically obvious). Acidemia (low pH) and alkalemia (high pH) are terms reserved for derangements in blood pH only.d) Compensation for a primary disorder takes place when the other component in the H-H ratio changes as a result of the primary event; these compensatory changes are not classified by the terms used for the four primary acid-base disturbances.9-10 For example, a patient who hyperventilates (lowers PaCO2) solely as compensation for metabolic acidosis does not have a primary respiratory alkalosis but simply compensatory hyperventilation. This terminology helps separate diagnosable and treatable clinical disorders from derangements in acid-base that exist only because of the primary disorder.
e) Compensatory changes for acute respiratory acidosis 11 and alkalosis,12 and metabolic acidosis 13,14 and alkalosis,15,16 occur in a predictable fashion, making it relatively easy to spot the presence of a mixed disorder in many situations. For example, single acid-base disorders do not lead to normal pH. Two or more disorders can be manifested by normal pH when they are opposing, e.g., respiratory alkalosis and metabolic acidosis in a septic patient. Although pH can end up in the normal range (7.35-7.45) in single disorders of a mild degree when fully compensated, a truly normal pH with abnormal HCO3– and PaCO2 should make one think of two or more primary acid-base disorders. Similarly, a high pH in a case of acidosis or a low pH in a case of alkalosis signifies two or more primary disorders. f) Maximal respiratory compensation for a metabolic disorder takes about 12-24 hours and maximal renal compensation for a respiratory disorder takes up to several days. As a rule of thumb, in maximally compensated metabolic acidosis the last two digits of the pH approximate the PaCO2.17 For example, a patient with a disease causing uncomplicated metabolic acidosis over 24 hours’ duration, whose pH is 7.25, should have a PaCO2 equal or close to 25 mm Hg. In metabolic alkalosis respiratory compensation is more variable and there is no simple relationship by which to predict the final PaCO2.16 The mistake here was in not appreciating the patient’s lack of appropriate hyperventilation for a state of ketoacidosis, and therefore in not diagnosing her respiratory impairment (she was not wheezing on arrival to ER). Similar cases have been reported in the literature.18g) Acute, uncompensated respiratory alkalosis (acute hyperventilation) and acidosis (acute hypoventilation) cause predictable changes in pH and bicarbonate11,12 (Table IV). Bicarbonate increases slightly from the biochemical reaction of acutely retained CO2 and decreases when CO2 is acutely excreted;11,12 these changes are instantaneous and independent of any renal compensation. Extreme acute hyperventilation can lower the bicarbonate to about 15 mEq/L and extreme acute hypoventilation can raise it to about 29 mEq/L (Table IV); a bicarbonate value outside this range must indicate either a renal compensatory mechanism or a primary metabolic acid-base disorder. The biochemical changes in bicarbonate from acute shifts in PaCO2 point to another particularly useful clue to the presence of a mixed disorder: a higher- or lower-than- expected bicarbonate value with any change in PaCO2. Thus a slightly low HCO3– concentration in the presence of hypercapnia suggests a concomitant metabolic acidosis (e.g., PCO2 50 mm Hg, pH 7.27, HCO3– 22 mEq/L); a slightly elevated HCO3– in the presence of hypocapnia suggests a concomitant metabolic alkalosis (e.g. PCO2 30 mm Hg, pH 7.56, HCO3– 26 mEq/L).
h) The bicarbonate (or total CO2) should also be examined in relation to the other measured electrolytes, specifically to calculate the anion gap (AG). AG is the Na+ concentration minus (total CO2 + Cl–). The normal AG, 12 +/- 4 mEq/L, is an artifact of measurement since these three electrolytes are only the ones most commonly measured. (Since the value of K+ is small and relatively constant it is not usually used to calculate the AG; if K+ is used then the normal AG is about 16 +/- 4 mEq/L). If all the serum anions and cations were measured anions would equal cations and there would be no anion gap. The importance of the anion gap is that it can help both to diagnose the presence of a metabolic acidosis and characterize its cause. Thus, regardless of pH an elevated AG suggests a metabolic acidosis from unmeasured organic anions, e.g., lactic acidosis or ketoacidosis;19-21 the higher the AG the more likely it reflects an organic acidosis.19 On the other hand a normal AG in a patient with metabolic acidosis indicates a hyperchloremic acidosis, most commonly from renal or gastrointestinal bicarbonate loss, e.g., renal tubular acidosis or diarrhea. |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||