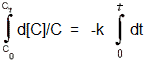Pharmacokinetics - First Order Rate Equation |
Derivation by David McAuley, Pharm D. |
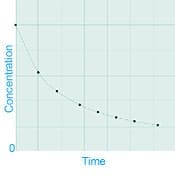 By definition, a first order process can be described as follows: [The rate of change in concentration versus time is directly proportional to the concentration 'C' at any point along the curve]. Note: if you graph the log of the concentration versus time, a linear graph will result. Using the concept of variation in relation to proportionality you get: |
Application |
| Additional background information can be found here. |